来写一个softmax求导的推导过程,不仅可以给自己理清思路,还可以造福大众,岂不美哉~
softmax经常被添加在分类任务的神经网络中的输出层,神经网络的反向传播中关键的步骤就是求导,从这个过程也可以更深刻地理解反向传播的过程,还可以对梯度传播的问题有更多的思考。
softmax 函数
softmax(柔性最大值)函数,一般在神经网络中, softmax可以作为分类任务的输出层。其实可以认为softmax输出的是几个类别选择的概率,比如我有一个分类任务,要分为三个类,softmax函数可以根据它们相对的大小,输出三个类别选取的概率,并且概率和为1。
softmax函数的公式是这种形式:
S
i
=e
z
i
∑
k
e
z
k
Si=ezi∑kezk
S
i
Si代表的是第i个神经元的输出。
ok,其实就是在输出后面套一个这个函数,在推导之前,我们统一一下网络中的各个表示符号,避免后面突然出现一个什么符号懵逼推导不下去了。
首先是神经元的输出,一个神经元如下图:
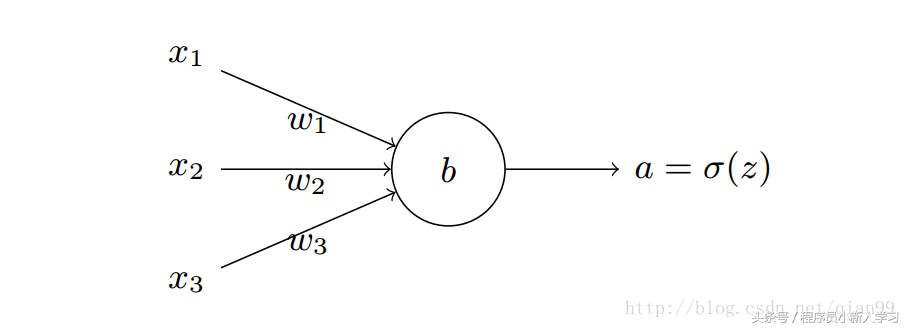
神经元的输出设为:
z
i
=∑
j
w
ij
x
ij
+b
zi=∑jwijxij+b
其中w
ij
wij是第i
i个神经元的第j
j个权重,b
b是偏移值。z
i
zi表示该网络的第i
i个输出。
给这个输出加上一个softmax函数,那就变成了这样:
a
i
=e
z
i
∑
k
e
z
k
ai=ezi∑kezk
a
i
ai代表softmax的第i个输出值,右侧就是套用了softmax函数。损失函数 loss function
在神经网络反向传播中,要求一个损失函数,这个损失函数其实表示的是真实值与网络的估计值的误差,知道误差了,才能知道怎样去修改网络中的权重。
损失函数可以有很多形式,这里用的是交叉熵函数,主要是由于这个求导结果比较简单,易于计算,并且交叉熵解决某些损失函数学习缓慢的问题。交叉熵的函数是这样的:
C=−∑
i
y
i
lna
i
C=−∑iyilnai
其中y
i
yi表示真实的分类结果。
到这里可能嵌套了好几层,不过不要担心,下面会一步步推导,强烈推荐在纸上写一写,有时候光看看着看着就迷糊了,自己边看边推导更有利于理解~最后的准备
在我最开始看softmax推导的时候,有时候看到一半不知道是怎么推出来的,其实主要是因为一些求导法则忘记了,唉~
所以这里把基础的求导法则和公式贴出来~有些忘记的朋友可以先大概看一下:


推导过程
好了,这下正式开始~
首先,我们要明确一下我们要求什么,我们要求的是我们的loss对于神经元输出(z
i
zi)的梯度,即:
∂C
∂z
i
∂C∂zi
根据复合函数求导法则:
∂C
∂z
i
=∂C
∂a
j
∂a
j
∂z
i
∂C∂zi=∂C∂aj∂aj∂zi
有个人可能有疑问了,这里为什么是a
j
aj而不是a
i
ai,这里要看一下softmax的公式了,因为softmax公式的特性,它的分母包含了所有神经元的输出,所以,对于不等于i的其他输出里面,也包含着z
i
zi,所有的a
a都要纳入到计算范围中,并且后面的计算可以看到需要分为i=j
i=j和i≠j
i≠j两种情况求导。
下面我们一个一个推:
∂C
∂a
j
=∂(−∑
j
y
j
lna
j
)
∂a
j
=−∑
j
y
j
1
a
j
∂C∂aj=∂(−∑jyjlnaj)∂aj=−∑jyj1aj
第二个稍微复杂一点,我们先把它分为两种情况:
①如果i=j
i=j:
∂a
i
∂z
i
=∂(e
z
i
∑
k
e
z
k
)
∂z
i
=∑
k
e
z
k
e
z
i
−(e
z
i
)
2
(∑
k
e
z
k
)
2
=(e
z
i
∑
k
e
z
k
)(1−e
z
i
∑
k
e
z
k
)=a
i
(1−a
i
)
∂ai∂zi=∂(ezi∑kezk)∂zi=∑kezkezi−(ezi)2(∑kezk)2=(ezi∑kezk)(1−ezi∑kezk)=ai(1−ai)
②如果i≠j
i≠j:
∂a
j
∂z
i
=∂(e
z
j
∑
k
e
z
k
)
∂z
i
=−e
z
j
(1
∑
k
e
z
k
)
2
e
z
i
=−a
i
a
j
∂aj∂zi=∂(ezj∑kezk)∂zi=−ezj(1∑kezk)2ezi=−aiaj
ok,接下来我们只需要把上面的组合起来:
∂C
∂z
i
=(−∑
j
y
j
1
a
j
)∂a
j
∂z
i
=−y
i
a
i
a
i
(1−a
i
)+∑
j≠i
y
j
a
j
a
i
a
j
=−y
i
+y
i
a
i
+∑
j≠i
y
j
a
i
=−y
i
+a
i
∑
j
y
j
∂C∂zi=(−∑jyj1aj)∂aj∂zi=−yiaiai(1−ai)+∑j≠iyjajaiaj=−yi+yiai+∑j≠iyjai=−yi+ai∑jyj
最后的结果看起来简单了很多,最后,针对分类问题,我们给定的结果y
i
yi最终只会有一个类别是1,其他类别都是0,因此,对于分类问题,这个梯度等于:
∂C
∂z
i
=a
i
−y
i