前言科普:什么是滑动窗口算法
滑动问题包含一个滑动窗口,它是一个运行在一个大数组上的子列表,该数组是一个底层元素集合。
假设有数组 [a b c d e f g h ],一个大小为 3 的 滑动窗口 在其上滑动,则有:
[a b c] [b c d] [c d e] [d e f] [e f g] [f g h]
一般情况下就是使用这个窗口在数组的 合法区间 内进行滑动,同时 动态地 记录一些有用的数据,很多情况下,能够极大地提高算法地效率。
1. 滑动窗口最大值
题目来源于 LeetCode 上第 239 号问题:滑动窗口最大值。题目难度为 Hard,目前通过率为 40.5% 。
题目描述
给定一个数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口 k 内的数字。滑动窗口每次只向右移动一位。
返回滑动窗口最大值。
示例:
输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3 输出: [3,3,5,5,6,7] 解释: 滑动窗口的位置 最大值 --------------- ----- [1 3 -1] -3 5 3 6 7 3 1 [3 -1 -3] 5 3 6 7 3 1 3 [-1 -3 5] 3 6 7 5 1 3 -1 [-3 5 3] 6 7 5 1 3 -1 -3 [5 3 6] 7 6 1 3 -1 -3 5 [3 6 7] 7
题目解析
利用一个 双端队列,在队列中存储元素在数组中的位置, 并且维持队列的严格递减,,也就说维持队首元素是 **最大的 **,当遍历到一个新元素时, 如果队列里有比当前元素小的,就将其移除队列,以保证队列的递减。当队列元素位置之差大于 k,就将队首元素移除。
补充:什么是双端队列(Dqueue)
Deque 的含义是 “double ended queue”,即双端队列,它具有队列和栈的性质的数据结构。顾名思义,它是一种前端与后端都支持插入和删除操作的队列。
Deque 继承自 Queue(队列),它的直接实现有 ArrayDeque、LinkedList 等。
动画描述

动画描述 Made by Jun Chen
代码实现
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
//有点坑,题目里都说了数组不为空,且 k > 0。但是看了一下,测试用例里面还是有nums = [], k = 0,所以只好加上这个判断
if (nums == null || nums.length < k || k == 0) return new int[0];
int[] res = new int[nums.length - k + 1];
//双端队列
Deque<Integer> deque = new LinkedList<>();
for (int i = 0; i < nums.length; i++) {
//在尾部添加元素,并保证左边元素都比尾部大
while (!deque.isEmpty() && nums[deque.getLast()] < nums[i]) {
deque.removeLast();
}
deque.addLast(i);
//在头部移除元素
if (deque.getFirst() == i - k) {
deque.removeFirst();
}
//输出结果
if (i >= k - 1) {
res[i - k + 1] = nums[deque.getFirst()];
}
}
return res;
}
}
2. 无重复字符的最长子串
题目来源于 LeetCode 上第 3 号问题:无重复字符的最长子串。题目难度为 Medium,目前通过率为 29.0% 。
题目描述
给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
题目解析
建立一个256位大小的整型数组 freg ,用来建立字符和其出现位置之间的映射。
维护一个滑动窗口,窗口内的都是没有重复的字符,去尽可能的扩大窗口的大小,窗口不停的向右滑动。
- (1)如果当前遍历到的字符从未出现过,那么直接扩大右边界;
- (2)如果当前遍历到的字符出现过,则缩小窗口(左边索引向右移动),然后继续观察当前遍历到的字符;
- (3)重复(1)(2),直到左边索引无法再移动;
- (4)维护一个结果res,每次用出现过的窗口大小来更新结果 res,最后返回 res 获取结果。
动画描述
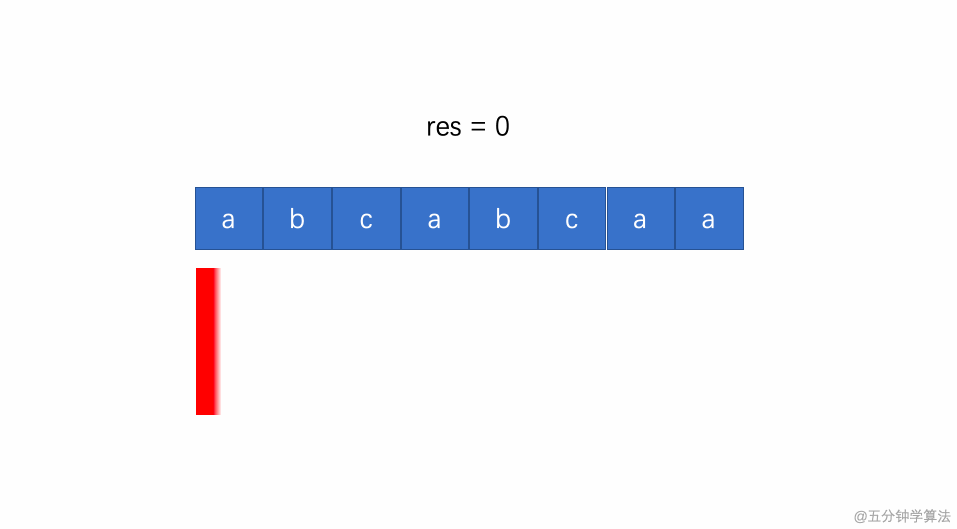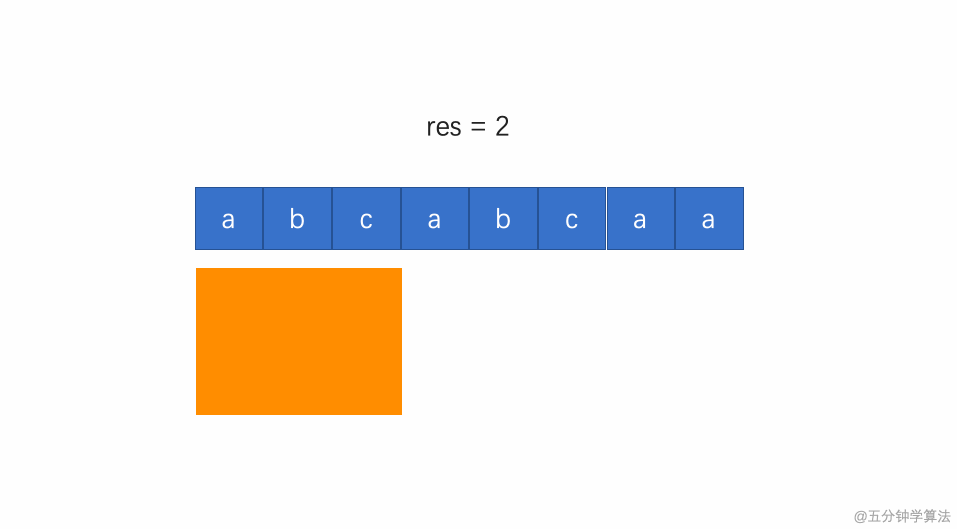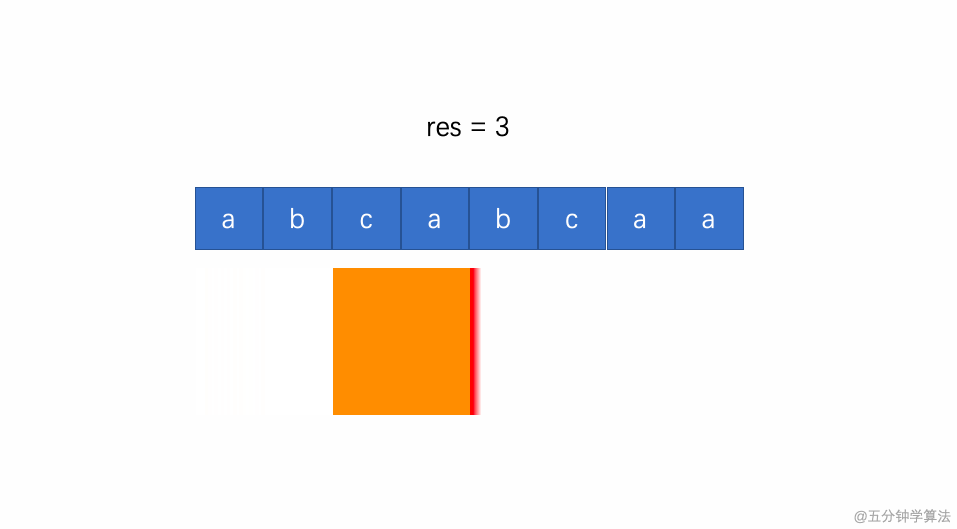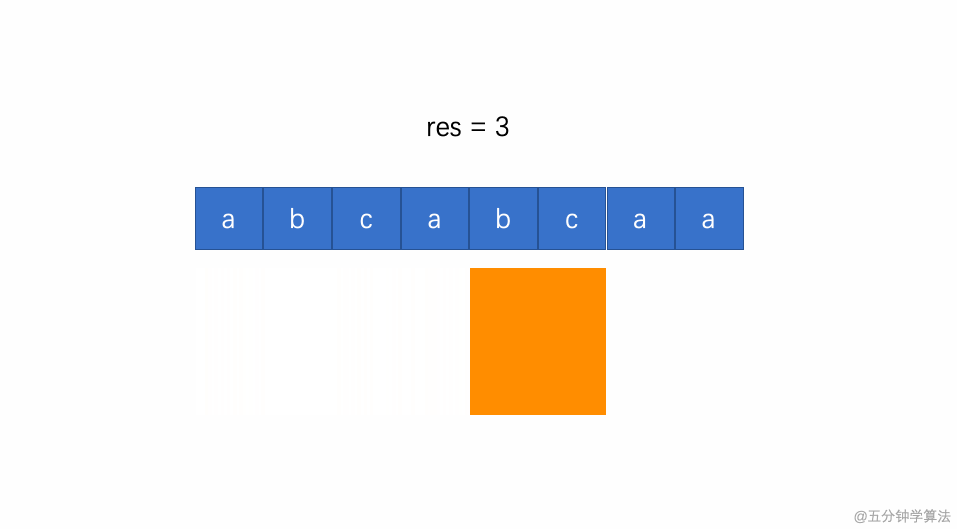
动画描述
代码实现
// 滑动窗口
// 时间复杂度: O(len(s))
// 空间复杂度: O(len(charset))
class Solution {
public:
int lengthOfLongestSubstring(string s) {
int freq[256] = {0};
int l = 0, r = -1; //滑动窗口为s[l...r]
int res = 0;
// 整个循环从 l == 0; r == -1 这个空窗口开始
// 到l == s.size(); r == s.size()-1 这个空窗口截止
// 在每次循环里逐渐改变窗口, 维护freq, 并记录当前窗口中是否找到了一个新的最优值
while(l < s.size()){
if(r + 1 < s.size() && freq[s[r+1]] == 0){
r++;
freq[s[r]]++;
}else { //r已经到头 || freq[s[r+1]] == 1
freq[s[l]]--;
l++;
}
res = max(res, r-l+1);
}
return res;
}
};
3. 存在重复元素 II
题目来源于 LeetCode 上第 219 号问题:存在重复元素 II。题目难度为 Easy,目前通过率为 33.9% 。
题目描述
给定一个整数数组和一个整数 k,判断数组中是否存在两个不同的索引 i 和 j,使得 nums [i] = nums [j],并且 i 和 j 的差的绝对值最大为 k。
示例 1:
输入: nums = [1,2,3,1], k = 3 输出: true
示例 2:
输入: nums = [1,0,1,1], k = 1 输出: true
示例 3:
输入: nums = [1,2,3,1,2,3], k = 2 输出: false
题目解析
使用用滑动窗口与查找表来解决。
- 设置查找表record,用来保存每次遍历时插入的元素,record的最大长度为k
- 遍历数组nums,每次遍历的时候在record查找是否存在相同的元素,如果存在则返回true,遍历结束
- 如果此次遍历在record未查找到,则将该元素插入到record中,而后查看record的长度是否为k + 1
- 如果此时record的长度是否为k + 1,则删减record的元素,该元素的值为nums[i - k]
- 如果遍历完整个数组nums未查找到则返回false
动画描述
动画描述
代码实现
// 时间复杂度: O(n)
// 空间复杂度: O(k)
class Solution {
public:
bool containsNearbyDuplicate(vector<int>& nums, int k) {
if(nums.size() <= 1) return false;
if(k <= 0) return false;
unordered_set<int> record;
for(int i = 0 ; i < nums.size() ; i ++){
if(record.find(nums[i]) != record.end()){
return true;
}
record.insert(nums[i]);
// 保持record中最多有k个元素
// 因为在下一次循环中会添加一个新元素,使得总共考虑k+1个元素
if(record.size() == k + 1){
record.erase(nums[i - k]);
}
}
return false;
}
};
4. 长度最小的子数组
题目来源于 LeetCode 上第 209 号问题:长度最小的子数组。题目难度为 Medium,目前通过率为 37.7% 。
题目描述
给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的连续子数组。如果不存在符合条件的连续子数组,返回 0。
示例:
输入: s = 7, nums = [2,3,1,2,4,3] 输出: 2 解释: 子数组 [4,3] 是该条件下的长度最小的连续子数组。
题目解析
定义两个指针 left 和 right ,分别记录子数组的左右的边界位置。
- (1)让 right 向右移,直到子数组和大于等于给定值或者 right 达到数组末尾;
- (2)更新最短距离,将 left 像右移一位, sum 减去移去的值;
- (3)重复(1)(2)步骤,直到 right 到达末尾,且 left 到达临界位置
动画描述
设置滑动窗口的长度为 0 ,位于数轴的最左端。
1 .滑动窗口右端 R 开始移动,直到区间满足给定的条件,也就是和大于 7 ,此时停止于第三个元素 2,当前的最优长度为 4
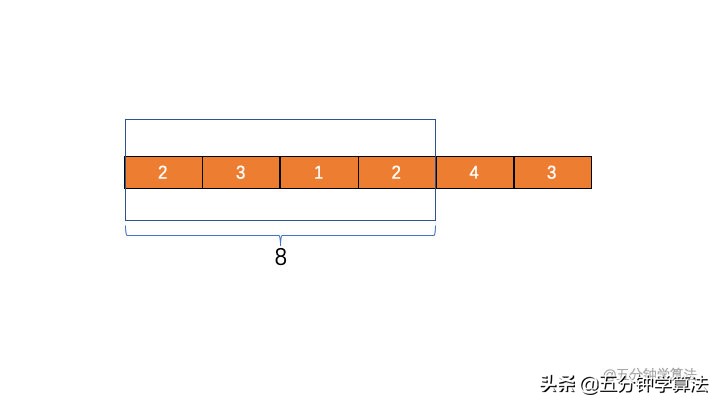
图 1
2. 滑动窗口左端 L 开始移动,缩小滑动窗口的大小,停止于第一个元素 3,此时区间和为 6,使得区间和不满足给定的条件(此时不大于 7)
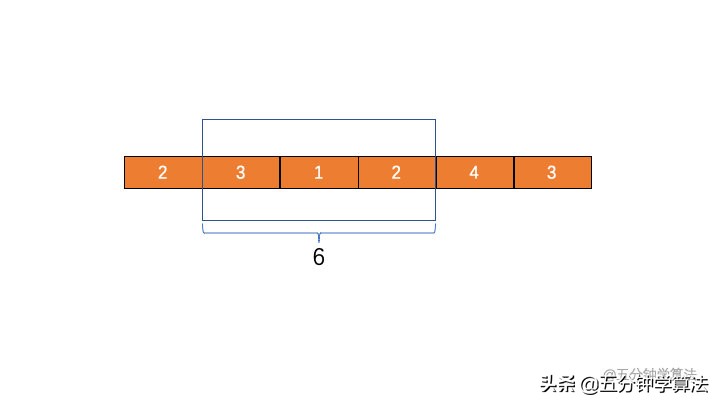
图片 2
3. 滑动窗口右端 R 继续移动,停止于第四个元素 4,此时和位 10 ,但最优长度仍然为 4
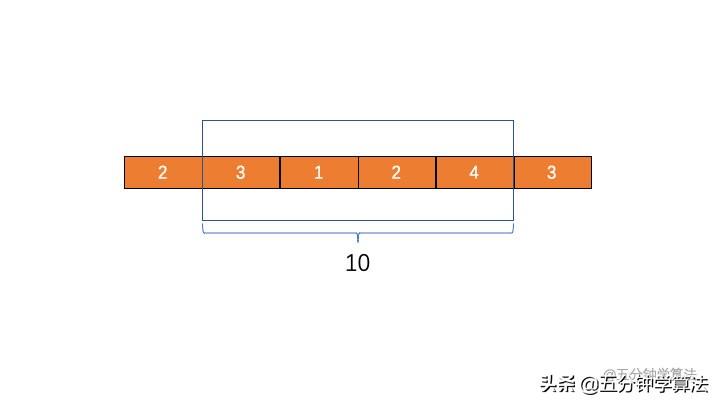
图片 3
代码实现
// 滑动窗口的思路
// 时间复杂度: O(n)
// 空间复杂度: O(1)
class Solution {
public int minSubArrayLen(int s, int[] nums) {
int l= 0,r = -1; // nums[l...r]为我们的滑动窗口
int sum = 0;
int result = nums.length + 1;
while (l < nums.length){ // 窗口的左边界在数组范围内,则循环继续
if( r+1 <nums.length && sum < s){
r++;
sum += nums[r];
}else { // r已经到头 或者 sum >= s
sum -= nums[l];
l++;
}
if(sum >= s){
result = (r-l+1) < result ? (r-l+1) : result ;
}
}
if(result==nums.length+1){
return 0;
}
return result;
}
}