在前两篇文章(《如何使用SPSS进行相关性分析(一)》、《如何使用SPSS进行相关性分析(二)》),我们介绍了相关关系的基本概念,并基于实际案例,使用SPSS对两个定类变量、两个定序变量进行了相关性分析。今天将继续基于实际案例来介绍其他变量类型的相关性分析:
(1)定距变量(连续型变量)间的相关性分析;
(2)定类变量和定距变量的相关性分析.
连续型变量的相关性分析
定距变量,即连续型变量之间的关系,我们一般使用线性相关分析的方法进行分析测量。
对于连续型变量来说,可以通过线性回归分析来以自变量(X)的数值来估计因变量(Y)的值,即构建线性回归模型来对未知的因素进行预测。但进行回归分析的前提是,变量之间必须存在相关关系。
我们初中曾学过的一元二次方程,即是简单线性回归模型的简写 Y=bX+a。其中,b值表示了自变量X对因变量Y的影响大小和方向,是一个分析不对称相关关系的统计方法。但b值的大小没有上限,要根据变量的衡量单位来定,因此很少被用来衡量连续型变量之间的相关程度。
在连续型变量的相关性分析中,我们主要使用皮尔逊(Pearson)的积矩相关系数(简写为 r)来测量连续型变量之间的相关大小和方向。
r 系数与b 系数的不同地方在于,r系数假定X与Y的关系是对称的,而且r的统计值范围是[-1,1]。r系数值越大,就表示线性回归方程式的预测能力越强。r^2称为决定系数(coefficient of determination),反映在某个变量的变化中有多少是受另一个变量的变化所决定。
在社会研究中,要先计算 r 系数值,即先判断变量之间是否存在相关关系,才能决定是否运用线性回归分析法来预测数值。如果r系数值很小,即相关性很弱或者不相关,那么就不要用线性回归方程式来预测,因为这样所犯的误差会很大。
通过皮尔逊(Pearson)方法测量出变量间的相关性大小后,还需要进行显著性检验,以确定基于随机样本数据计算的相关系数是否能推论总体。
接下来,我们将以 "休闲调查.sav" 的数据进行实际案例操作。
研究问题:住房面积和家庭月收入的相关关系是怎样的?
针对该研究问题,SPSS的分析操作如下过程。
(一)打开双变量相关分析对话框,添加变量
操作路径:工具栏“分析”——相关——双变量
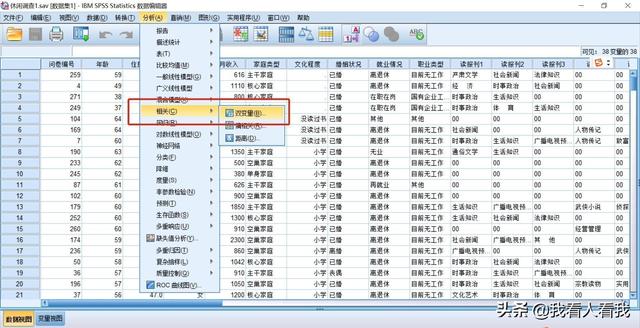
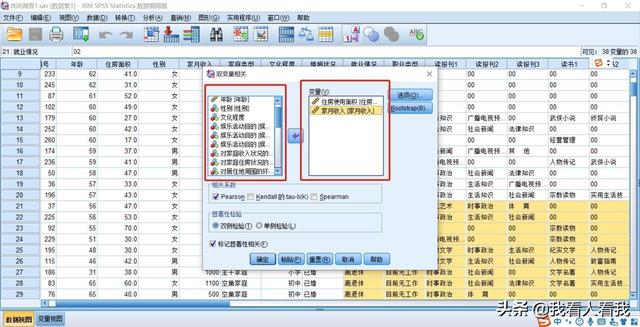
将需要分析的“住房使用面积”和“家庭月收入”从左侧的原变量窗口添加到右侧的目标变量窗口。
(二)确定统计量
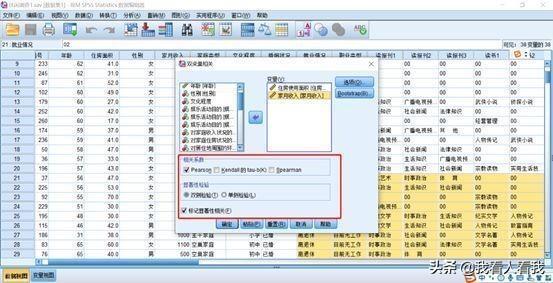
在变量窗口下,【相关系数】我们这里选择Pearson,前文已经说明,这里不再赘述;【显著性检验】即检验样本是否能够推论总体,这里选择双侧检验(关于单侧检验和双侧检验,后面有机会再详细介绍);【标记显著性相关】的作用是在显著性水平为0.05和为0.01时以星号进行标记,当显著性水平为0.05时标记一个星号,为0.01时标记两个星号。
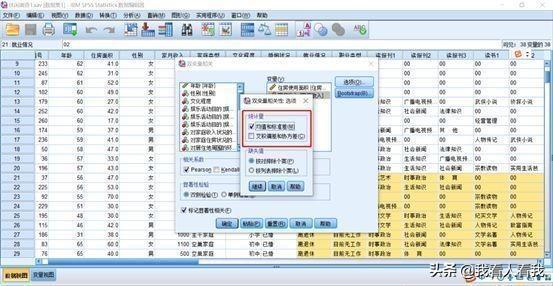
打开对话框右侧的【选项】功能,主要关注【统计量】框中的选项,这里我们想输出“均值和标准差”。
最后,单机确定,交给系统运行计算。
(三)解读统计分析结果
系统主要输出了两个统计结果:描述性统计量表和相关性表。
1. 描述性统计量
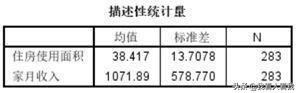
从这个表中,我们可以看到所分析的变量的均值、标准差和样本量。这个就大概看下就好,关键是相关性表
2. 相关性表
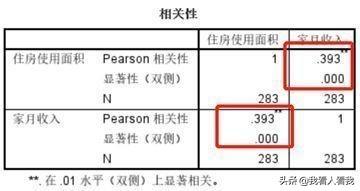
这里主要看红框里的值。从表中可以看到,住房使用面积和家庭月收入存在相关关系,其相关系数为0.393,呈现中度相关性,且在0.01的显著性水平上显著,即样本数据中的这个相关性在总体中一样有效。
定类变量和定距变量的相关性分析
在分析定类变量与定距变量的相关关系时,我们可以使用相关比率来测量相关性程度。
相关比率,又称为eta平方系数,简写为E^2,是以一个定类变量X为自变量,以一个定距变量Y为因变量,根据自变量的每一个值来预测或估计因变量的均值。
由于相关比率计算过程中,有一个变量是定类变量,所以eta系数值(E)没有负数,取值范围为[0,1]。E^2具有消减误差比例的意义。
倘若所研究的是一个随机样本,要想将相关性结果推论总体,则可通过单因素方差分析(one-way analysis of variance)中的F检验判断是否可行。F检验的逻辑是通过计算各组总体中的均值是否相等,如果相等,说明总体中自变量对因变量没有显著影响;如果各组总体的均值不全相等,则说明总体中自变量对因变量的影响是显著的。
实际上,对于严谨的研究来说,在进行单因素方差分析之前还应该要做方差齐性检验,因为使用单因素方差分析不仅要求各个类别的样本是随机且独立的,而且还要求各个总体的方差要相等。由于单因素方差和方差齐性检验有点复杂,这里我们就不做展开,后面再专门对方差分析进行介绍。
接下来,我们将基于“休闲调查.sav”的数据进行实际案例操作。
研究问题:不同文化程度的人的住房面积是否存在差异?
针对该研究问题,SPSS的分析操作如下过程。
(一)打开对话框,添加变量
操作路径:工具栏“分析”——比较均值——均值
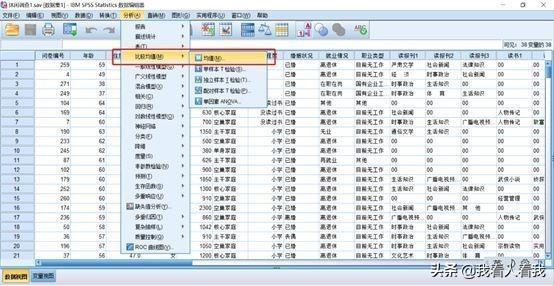
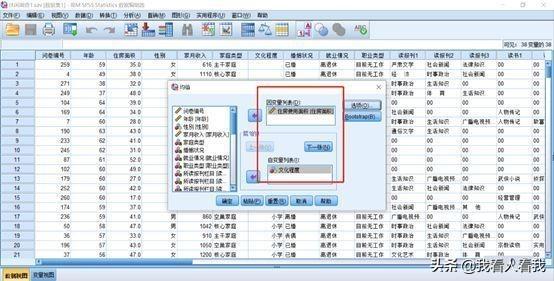
从研究问题来看,实际上是把“文化程度”当作了自变量,而将“住房使用面积”当作了因变量。因此,在变量窗口中,我们需要将“住房使用面积”变量放到因变量列表窗口中,将“文化程度”变量添加到自变量列表窗口中。
(二)确定统计量
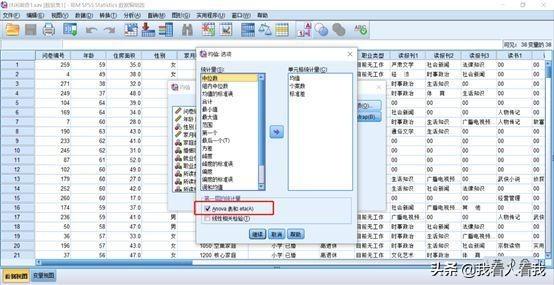
主要关注“第一层的统计量”框中的“ANOVA表和eta”。ANOVA即单因素方差分析,对样本数据推论总体进行显著性检验,输出的是ANOVA表;eta即计算相关性大小的方法。
(三)解读统计结果
最后输出的结果中,我们主要看ANOVA表和相关性度量表即可。
1. ANOVA表

从表中我们可以知道,单因素方差分析告诉我们,F检验的显著性水平为0.05,也就是说,单因素方差分析的原假设“总体中各个类别的均值相等”成立的情况下,F值(2.129)出现的概率为0.05,属于小概率事件,所以我们应该拒绝原假设,即说明,总体中不同文化程度的人的住房面积是有显著差异的,即总体中文化程度和住房面积存在相关关系。
那么,文化程度和住房面积之间的相关程度有多大呢?这里就需要看相关比率,即eta平方值。
2. 相关性度量
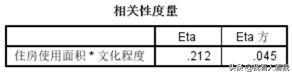
从表中可以得知,eta平方值为0.045,这是什么水平呢,在实际研究中,如何判断eta平方值的程度?一般来说,eta平方小于0.06时,表明变量之间的相关程度比较微弱,这种程度只存在统计显著的意义,而缺乏实际应用价值;eta平方大于0.06,小于0.16时,表明变量之间有中度的相关关系;当eta平方大于0.16时,表明变量之间存在强相关。
因此,eta平方值仅为0.045,说明文化程度与住房面积之间虽然存在相关性,但相关程度很弱,实际意义不大。