导读
做图像处理的同学应该经常都会用到图像的缩放,我们都知道图片存储的时候其实就是一个矩阵,所以在对图像进行缩放操作的时候,也就是在对矩阵进行操作,如果想要将图片放大,这里我们就需要用到过采样算法来扩大矩阵,如果想要缩小图片就使用欠采样。
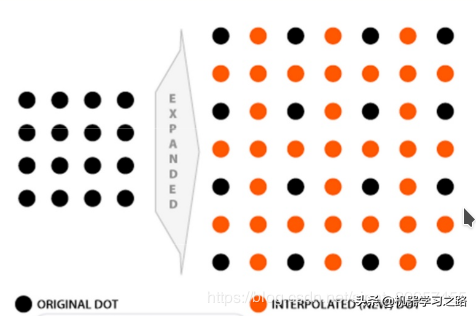
如上图所示,左图是原图像矩阵,右图是扩大后的图像矩阵,右图中的橙色点表示的是矩阵扩大之后通过插值算法填充的像素值。所以,这篇文章我们主要探讨的就是如何来通过插值算法来填充像素值
相关函数介绍
在opencv中提供了一个resize函数用来调整图像的大小,里面提供了好几种不同的插值算法,如下图所示
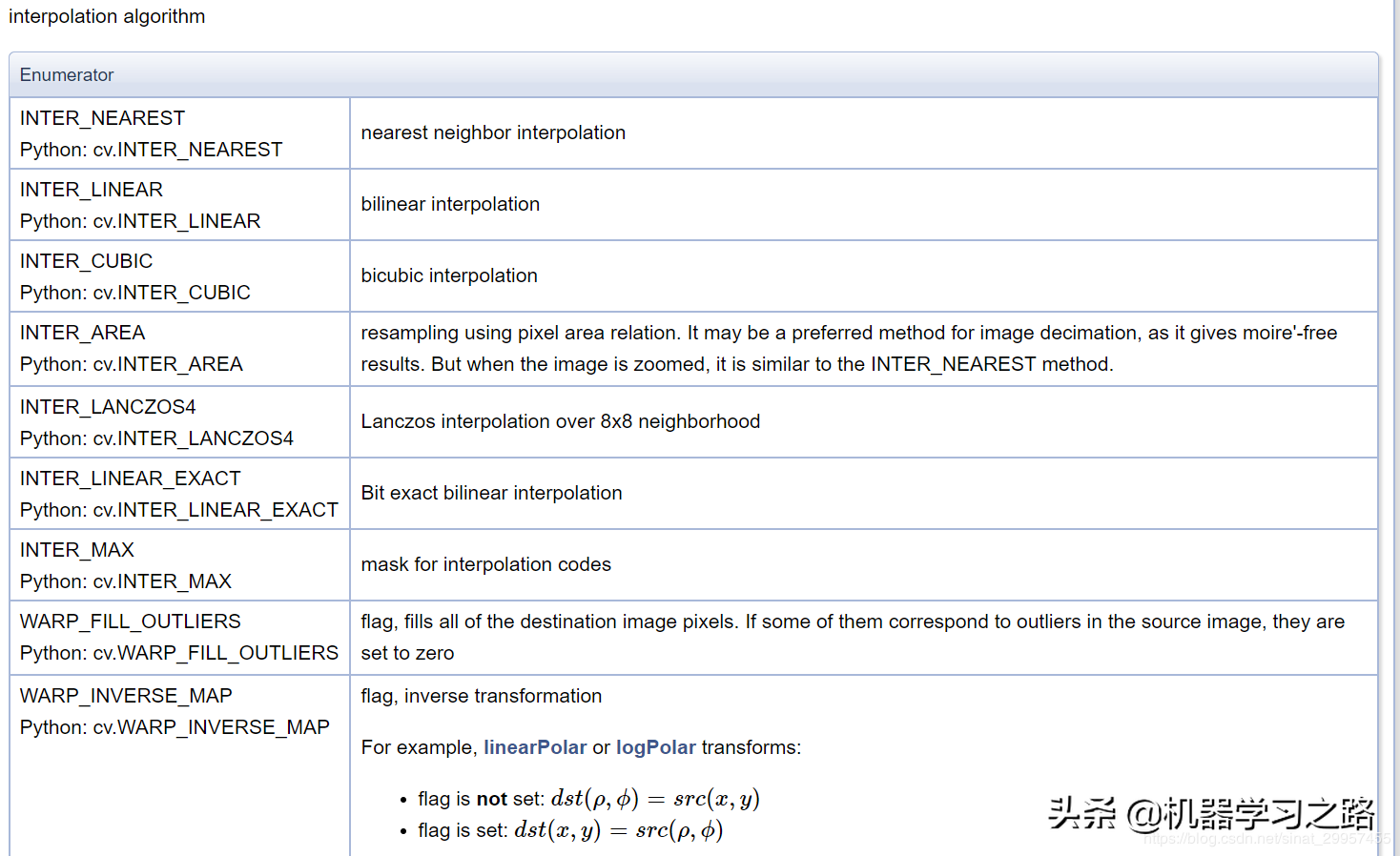
这里我们主要介绍最常用的前5中插值算法,最后两种插值算法主要是应用在仿射变换中,cv.WARP_FILL_OUTLIERS在从src到dst变换的时候可能会出现异常值,通过这个设定可以将异常值的像素置0。而cv.WARP_INVERSE_MAP是应用在仿射变换的逆变换,从dst到src的变换,关于仿射变换的更多资料可以参考我的上篇文章一文搞懂仿射变换
插值算法效果对比
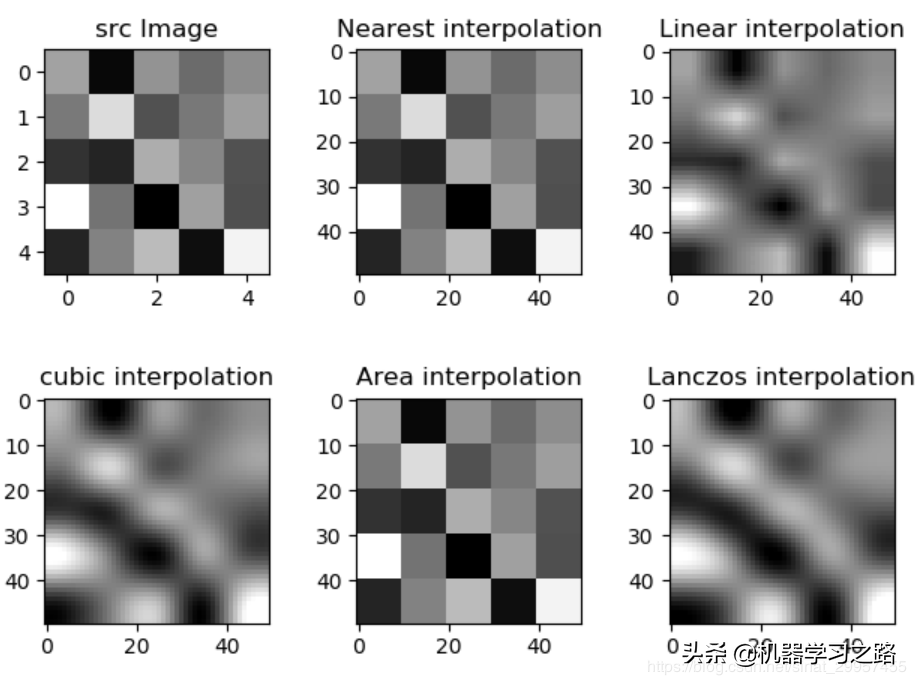
我们通过随机生成一个5×5的图片,然后通过不同的插值算法将其放大10倍之后,来对比最终图片的效果。
如果大家觉得灰度图不方便观察,我们可以通过设置plt.imshow的cmap参数来控制颜色,matplotlib提供了几种不同的类别的色彩映射方式
cmap的类别
-
Sequential
通常使用单一的色调,逐渐增加亮度和颜色,可以用来表示有序的信息
通过改变两种不同的颜色的亮度和饱和度,在中间以不饱和的颜色相遇,通常来用绘制具有关键的中间值或者数据偏离零的信息
改变两种不同颜色的亮度,在中间和开始/结束以不饱和的颜色相遇,应用于在端点出环绕的信息。
用于表示没有关系和排序的信息

同上
这里我们为了方便观察不同插值算法之间的区别,我们可以选用杂色来来观察,这里我就随机选用了Set1,只需要将上面代码中的cmap改成了Set1即可
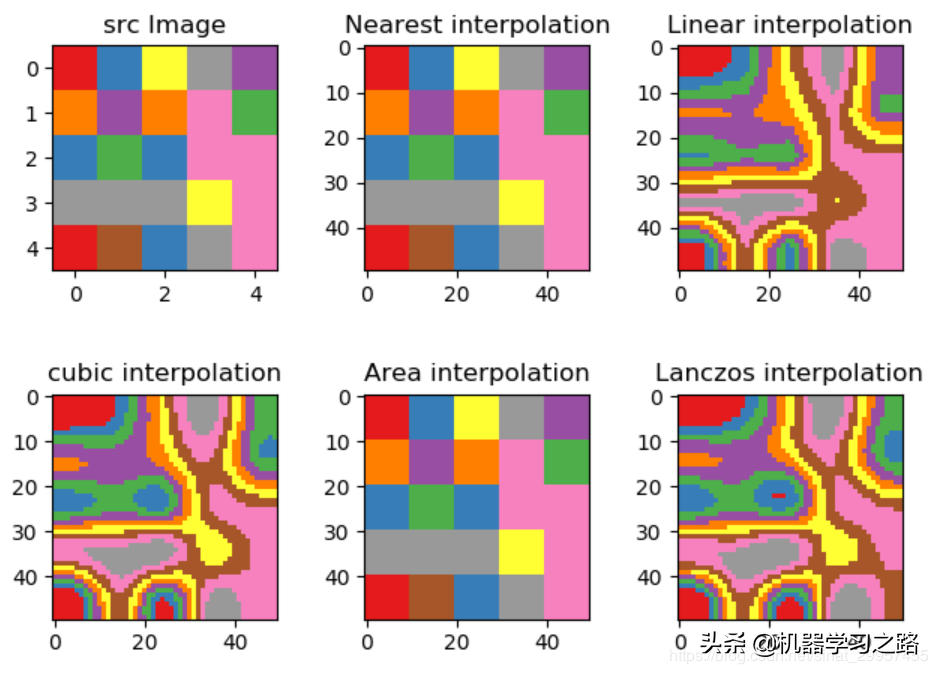
通过初步观察不同插值算法后的效果图片我们可以发现,最近邻插值和区域插值算法的效果,而线性插值、三次样条插值、Lanczos插值整体效果看起来差不多,不过细节部分还是有所差别,接下来我们就从这几种插值算法来分析一下。
最近邻插值(Nearest Interpolation)
最近邻插值也称近端插值,是一种在一维或多维空间上进行多变元插值的简单方法。插值是一种通过已知的、离散的数据点,在范围内推求新数据点的过程或方法。最近邻插值算法选择距离所求数据点最近点的值,并且根本不考虑其他相邻点的值,从而产生一个分段常数的内插值来作为所求数据点的值。

如上图所示,黑色的×表示需要插入的值,它会选择距离它最近的P(x 1,y)的值来作为它的值。
如果距离四个点的距离都相等,最近邻插值会如何选择?

通过上图不难发现,当插入的值距离四个点都相等时,会选择距离最近的左上角的值,这是
因为图像坐标系的原点位于左上角。
线性插值(Linear interpolation)
这里的线性插值其实是指双线性插值,这种插值算法也是resize函数中默认使用的插值算法。
双线性插值,也被称为双线性内插。双线插值是对线性插值在二维坐标系上的扩展,用于对双变量函数进行插值,其核心思想是在两个方向上分别进行一次线性插值。为了帮助大家更好的理解双线性插值算法,我们先来看线性插值
假设我们已知坐标(x0,y0)与(x1,y1),我们想要得到该区间[x0,x1上任意位置x所对应y的值,如下图所示
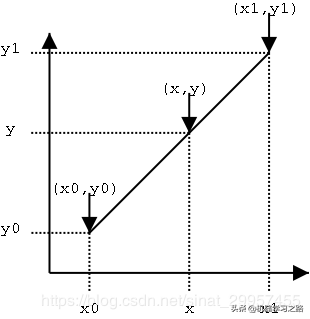
我们可以求出直线的方程,然后将x坐标代入到方程就可以求出对应的y值,通过直线方程的两点式可以得到
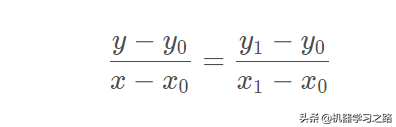
然后我们根据已知的x,将其代入上式可得

在了解线性插值以后,我们再来看看双线性插值
假如我们想得到未知函数fff在点P=(x,y)的值,假设我们已知函数f在Q11=(x1,y1),Q12=(x1,y2),Q21=(x2,y1)及Q22=(x2,y2)四个点的值
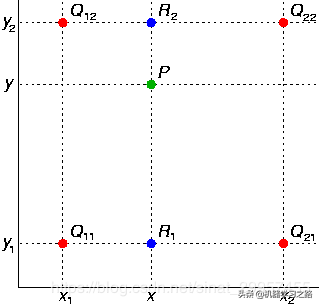
首先在x方向进行线性插值,利用Q11和Q21可以求得R1的y值,利用Q12和Q22可以求得R2的y值
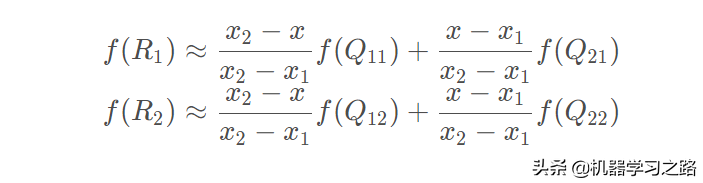
细心的同学也许发现了,这个插值好像与线性插值并不是一模一样的,所以我们用的是≈而非=,这里其实采用的是一种加权平均算法结合两点来计算其中一点的y值,主要是根据计算点距离两个端点在x方向上的距离来计算计算点y值所占的比例。
接下来,我们再利用已经计算出来的R1和R2来P点的插值,可得

仔细观察上面的公式不难发现,其实PPP点的值等于周围四个点与P点所构成的四个对角矩形面积的加权平均

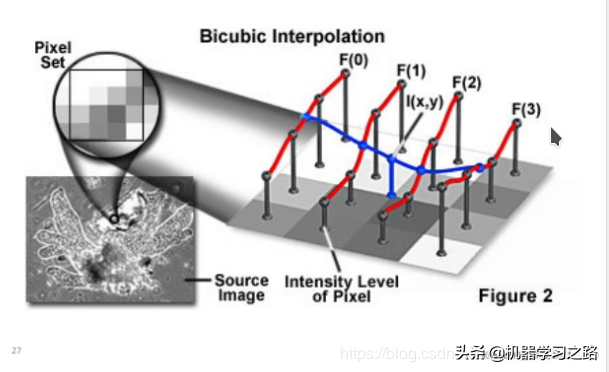
双三次插值(Bicubic interpolation)
双三次插值是一种更加复杂的插值算法,是二维空间中最常用的插值算法,相对双线性插值的图像边缘更加平滑,函数f在点(x,y)的值可以通过矩形网格中最近的十六个采样点的加权平均得到,这里需要使用两个多项式插值三次函数,每个方向使用一个。
双三次插值通过以下公式进行计算:
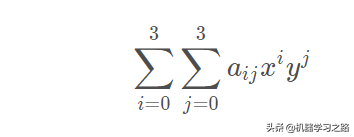
计算系数aij的过程依赖于插值数据的特性。如果已知插值函数的导数,常用的方法就是使用四个顶点的高度以及每个顶点的三个导数。一阶导数h′x与h′y表示x与y方向的表面斜率,二阶相互导数h''xy表示同时在x与y方向的斜率。这些值可以通过分别对x与y向量取微分得到。对于网格单元的每个顶点,将局部坐标(0,0)、(1,0)、(0,1)、(1,1)代入这些方程,再解这16个方程。
看了上面这段话之后,貌似还是不太好理解,接下来我们看一个例子,双三次插值常用的BiCubic函数如下图
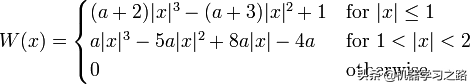
上式中的a取-0.5即可,函数图像如下
对待插值的像素点(x,y)(x,y可为浮点数),取其附近的4×4领域点(xi,yi)其中i,j=0,1,2,3。按下面的公式进行插值计算:
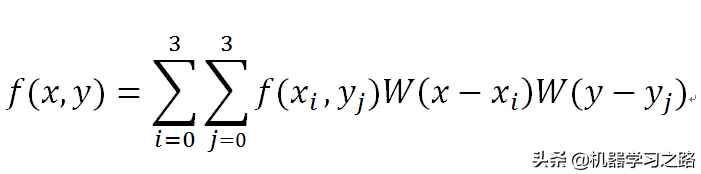
例如,我们需要求解P点值,在P点周围有16个点

首先,我们要求出当前像素与PPP点的距离,比如a00距离P(x u,y v)的距离为(1 u,1 v),那么我们可以得到a00对应的系数为(W(1 u),W(1 v)),所以a11的系数为(W(u),W(v)),a22的系数为(W(1−u),W(1−v)),a33的系数为W(2−u),W(2−v),同理可以得到剩下点的系数,再根据上面的函数就可以求出P点的值。
关于双三次插值函数更加详细介绍可以参考:论文
http://www.ncorr.com/download/publications/keysbicubic.pdf
区域插值(Area interpolation)
区域插值算法主要分两种情况,缩小图像和放大图像的工作原理并不相同。
-
缩小图像
如果图像缩小的比例是整数倍,在调用INTER_LINEAR_EXACT插值算法时,如果图像的宽和高的缩小比例都是2,而且图像的通道数不是2,实际上会调用INTER_AREA。在调用INTER_LINEAR时,如果图像的宽和高的缩小比例都是2,实际上是会调用INTER_AREA。
INTER_AREA实际上是个box filter,类似于均值滤波器。 -
放大图像
如果放大图像的比例是整数倍,与最近邻插值相似。如果放大的比例不是整数倍,则会采用线性插值。
Lanczos插值
Lanczos插值属于一种模板算法,需要通过计算模板中的权重信息来计算x对应的值。对于一维信息,假如我们输入的点集为X,那么,Lanczos对应有个窗口模板Window,窗口中每个位置的权重计算如下:
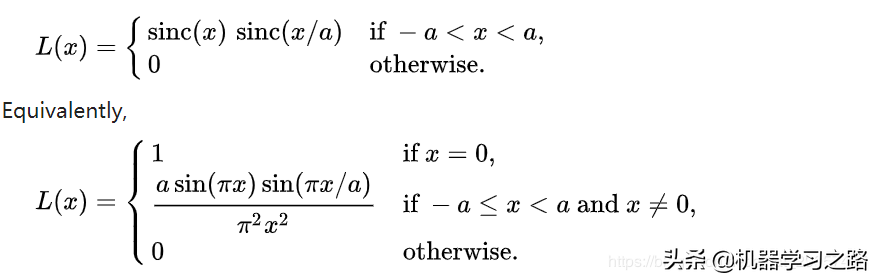
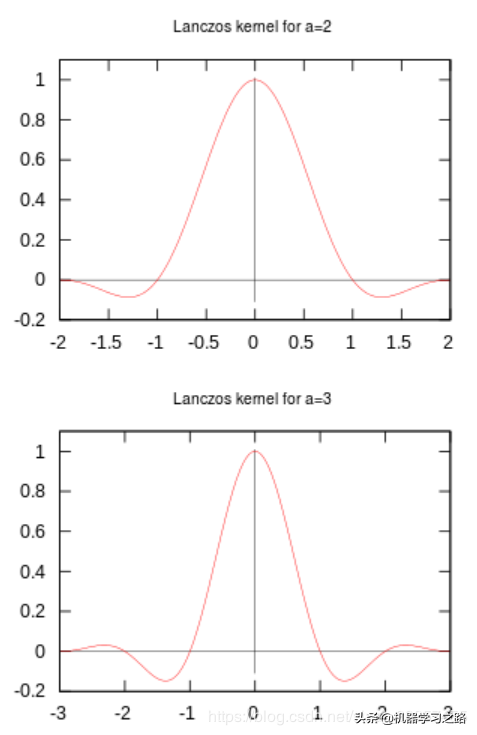
通常a取2或者3,当a=2时,该算法适应于图像缩小的插值。当a=3时,算法适用于图像放大的插值。根据计算出来的权重信息,然后再根据xxx即可求出对应的加权平均:
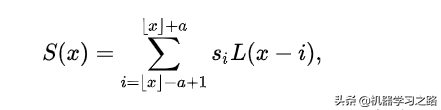
插值算法耗时比较
对于不同的插值算法,在缩放因子不同的时候,耗时会有所区别,具体对照如下表所示

总结
如果要缩小图像,推荐使用INTER_AREA插值效果最好,如果要放大图像,INTER_CUBIC效果最好,但是速度较慢,可以考虑使用INTER_LINEAR速度较快,效果也还不错。