在计算机中,负数都是以补码的形式存放的。而负数的补码正是正数的补码的相反数,由于我们只知道如何计算正数的二进制,所以在求负数的二进制的时候,应该先求负数的相反数的二进制(即正数的二进制),然后再求正数的二进制的相反数。具体计算过程如下:先求负数所对应的相反数(即正数)的二进制,然后再取反,再加1,就得到了负数的二进制,这也是负数在计算机中的存储形式。
如果反过来,则应该逆着算,具体步骤如下:现已知某负数的二进制,求该负数的十进制,则应该先将负数的二进制取反再加1,得到对应正数的二进制,然后再求该正数的十进制,最后取相反数,就得到了该负数的十进制。图示如下:
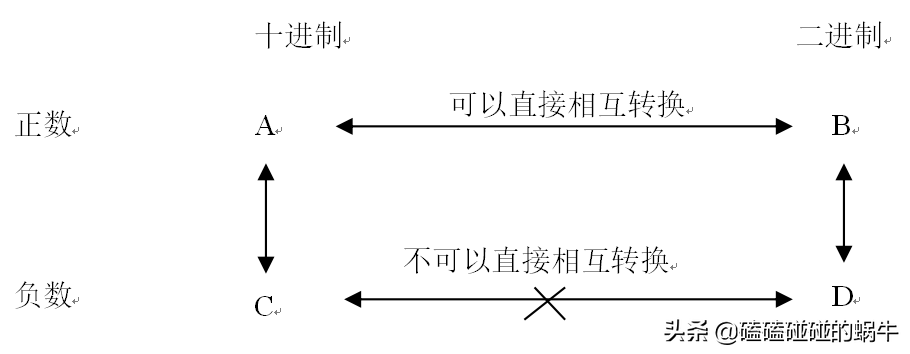
从上面的图可以看出,负数要求二进制,必须通过正数;反过来求,也必须通过正数。
注意:这里讲的二进制,都是指整数的补码。当我们看到一个补码时,如何判断它是正数还是负数呢,关键是看它的符号位(最高位),若为1则为负数,转换成十进制后还需取它相反数,若为0则为正数。
在以前的书籍中,反码和补码是这样说的:
求反码:对于正数,其反码和原码相同;对于负数,则将其原码的符号位保持不变,而将其他位按位取反(即将0换为1,将1换为0)。
求补码:对于正数,其补码和原码相同;对于负数,先求其反码,再在最低位加1(称为末位加1)。若对一补码再次求补,就又得到了对应的原码。
注意:“对应的原码”指的是正数的二进制或负数的二进制,若已经得到负数的补码,然后对其再一次求补,则会得到负数的原码,即负数的二进制。
负数的二进制,其实就是,在正数的二进制的最高位前面加一个符号位1。
但这种方法在使用时需要注意,在求负数的补码时,先要将负数转换成二进制,然后以该二进制为原码来去求补码。而在将负数转换成二进制的时候,其最高位(即符号位)一定是1,并且转换时不需要考虑数据的字节长度(即,需要多少位来表示这个数,那就用多少位);还有,将负数的二进制转换回负数时,其符号位是不算在内的,符号位只表示正负,不表示数值的大小。例如,求-128的补码:
-128的二进制是110000000(注意:-128占了9位,超出了一个字节),然后按照上面的规则求其补码,先求反码(符号位保持不变,其他位取反),再加1,结果为110000000,发现与原来一样,若用一个字节来存储,那就是10000000(把高位给截掉),也就是说,-128在计算机存储时是以10000000(补码)的形式存储的,在计算机中它就表示-128。
其实,以上两种计算负数补码的方法,本质上是一样的,因为在“取反加1”这一步中,两种方法都只是把负数的绝对值(即正数)取反加1,而并没有把符号位也取反;但这两种方法还是有所区别的,前一种方法在计算过程中直接把符号位给舍弃掉了,直接用正数取反加1后的结果的最高位来替代符号位;而后一种方法则并没有舍弃,所以在计算过程中需要加入符号位,但它只用来表示所存储的数是一个正数还是一个负数,在实际计算过程中它并不参与,在存储时符号位是会被舍弃的,不算在内,不管符号位是否超出了存储范围。